Question

What is the gauge pressure of the water flowing through the constricted segment?

Answer 1

`1.45atm`

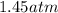
Step-by-step explanation

Parameters given:

Speed of water at point 1, v1 = 5.1 m/s

Diameter of pipe at point 1, d1 = 3.5 cm = 0.035 m

Pressure, P1 = 1.9 atm

Diameter of pipe at point 2, d2 = 2.4 cm = 0.024 m

Atmospheric pressure = 1.013 * 10^5 Pa

Density of water = 1000 kg/m^3

First, we have to find the speed of the water at the smaller end of the pipe. To do this, apply the Bernoulli continuity equation:

`A_1v_1=A_2v_2`

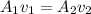
where A1 and A2 are the cross-sectional areas of the pipes at point 1 and point2 respectively.

Substituting the given values into the equation above:

`\begin{gathered} (\pi\cdot((0.035)/(2))^2)\cdot5.1=(\pi\cdot((0.024)/(2))^2)\cdot v_2 \\ \Rightarrow v_2=(0.0175^2\cdot5.1)/(0.012^2)^{} \\ v_2=10.85m\/s \end{gathered}`

Now, we have to apply Bernoulli's equation to find the pressure at the constricted segment:

`\begin{gathered} P_1+0.5\rho v^2_1=P_2+0.5\rho v^2_2 \\ \Rightarrow P_2=P_1+0.5\rho(v^2_1-v^2_2) \end{gathered}`

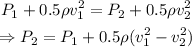
Substitute the known values into the equation and solve for P2, we have:

`\begin{gathered} P_2=(1.9)(1.013\cdot10^5)+(0.5)(1000)(5.1^2-10.85^2) \\ P_2=192,470+(500)(26.01-117.72)=192,470+(500)(-91.71) \\ P_2=192,470-45,855 \\ P_2=146,615Pa=(146615)/(1.013\cdot10^5)atm \\ P_2=1.45atm \end{gathered}`

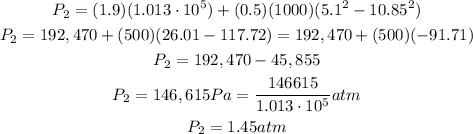
That is the answer.