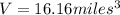Question

Find the volume of a right solid whose base is the figure shown on the left and whose height is 0.5 mile. Dimensions are in miles. Angles that look like right angles are right angles.

Answer 1

We can divide the given figure in 3 parts:

The area of the triangle is

`\begin{gathered} A_{\text{triangle}}=(1)/(2)4*5 \\ A_{\text{triangle}}=10miles^2 \end{gathered}`

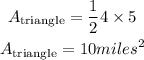
The area of the rectangle is

`\begin{gathered} A_{\text{rectangle}}=5*2.5 \\ A_{\text{rectangle}}=12.5miles^2 \end{gathered}`

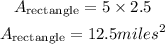
and the area of the semicircle is

`\begin{gathered} A_{\text{semicircle}}=(1)/(2)\pi(2.5)^2 \\ A_{\text{semicircle}}=9.8175miles^2 \end{gathered}`

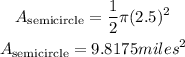
Then, the area of our figure is

`\begin{gathered} A=A_{\text{triangle}}+A_{\text{rectangle}}+A_{\text{semicircle}} \\ A=10+12.5+9.8175 \\ A=32.3175miles^2 \end{gathered}`

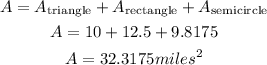
Now, the volume is given by

`V=0.5* A`

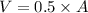
then,it yields

`V=0.5*32.3175\text{ }`

and, by rounding the the nearest cent, the volume is

`V=16.16miles^3`