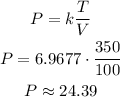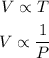
Therefore:
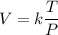
Where:
k = Constant of proportionality
T = Temperature
V = Volume
P = Pressure
A cylinder contains oxygen at a temperature of 310 degrees K and a pressure of 18 atmospheres in a volume of 120 liters. So:

Therefore, if the volume is decreased to 100 liters and the temperature is increased to 350 degrees K. The pressure will be: