The distribution of the number of daily requests is bell-shaped and has a mean of 51 and a standard deviation of 6.
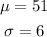
Empirical Rule:
The empirical rule states that
68% of all the observed data will fall within 1 standard deviation from the mean.
95% of all the observed data will fall within 2 standard deviations from the mean.
99.7% of all the observed data will fall within 3 standard deviations from the mean.
Using the empirical rule what is the approximate percentage of lightbulbs replacement requests numbering between 33 and 51.
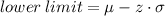
Using the above equation, let us find z (that is how many standard deviations away is out data from the mean)

That means that 99.7% of the lightbulbs replacement requests are found between 33 and 51 daily requests.
Since we have a bell-shaped distribution that is symmetrical around the mean,
99.7%/2 = 49.85%
49.85% of lightbulbs replacement requests are found between 33 and 51.