Question

Given:• EFGH is a rhombus• The perimeter of EFGH is 32EF70HGWhich is closest to the length of EG?5.57.51516

Answer 1

To calculate the length of EG, we need to make use of some of the properties of a rhombus.

A rhombus is a quadrilateral with four of its sides equal.

Also, the perimeter of a shape is the sum of all its outer sides.

Since the perimeter is 32, and the rhombus has 4sides, then each side will be;

`\begin{gathered} P=32 \\ \text{Each side will be;} \\ =(32)/(4) \\ =8 \\ \text{Hence,} \\ EF=FG=GH=HE=8 \end{gathered}`

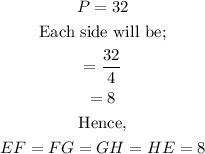
To find the diagonal EG, we use the diagonal property of a rhombus.

The diagonals of a rhombus bisect each other at 90 degrees. They are perpendicular to each other.

This means we can have a sketch as shown below cut from the rhombus.

From the sketch above,

`\begin{gathered} GH=8 \\ OG=x \\ EG=2x \end{gathered}`

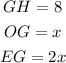
Using the trigonometric ratio of sine to get x,

`\begin{gathered} \sin =\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin 70=(x)/(8) \\ 0.9397=(x)/(8) \\ C\text{ ross multiplying,} \\ x=8*0.9397 \\ x=7.5176 \\ \text{Hence,} \\ OG=7.5176 \end{gathered}`

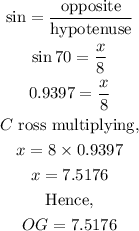
Since the diagonals of a rhombus bisect each other, the EG is twice the length of OG, because OG is half of EG.

`\begin{gathered} EG=2x \\ EG=2* OG \\ EG=2*7.5176 \\ EG=15.0352 \\ EG\approx15 \end{gathered}`

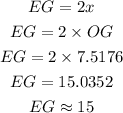
Therefore, the closest to the length of EG is 15.