The change in velocity Δv for an object that accelerates at a constant rate a during a time interval Δt is given by the equation:

On the other hand, if a force F acts on an object with mass m, the object will be accelerated by the force at a rate a given by:
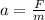
Replace F=150N and m=4kg to find the acceleration of the bowling ball:
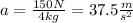
Next, replace a=37.5 m/s^2 and Δt=0.2s to find the change in velocity of the bowling ball:
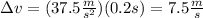
Therefore, the change in velocity is 7.5m/s.