Question

Pleasantburg has a population growth model of P(t) =at to the second power +bt+Po where Po is the initial population. Suppose that the future population of Pleasantburg T years after January 1, 2012 is described by the quadratic model P(t) =0.9t to the second power + 6t +23,000. What is the population of Pleasantburg on January 1, 2021? Round your answer to the nearest person.

Answer 1

Given that the population model growth of Pleasantburg is expressed as

`\begin{gathered} P(t)=at^2+bt+P_0\text{ ---- equation 1} \\ \text{where} \\ P_{0\text{ }}is\text{ the initial population} \end{gathered}`

Suppose that the population t years after January 1, 2012 is expressed as

`P(t)=0.9t^2+6t+23000\text{ ---- equation 2}`

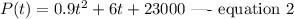
This implies that at the first year (January 1, 2012), t equals zero.

To solve for the population of Pleasentburg, we determine the value of t between January 1, 2012 and January 1, 2021.

The number of years between the two periods is 9 years.

Thus, substitute the value of 9 for into equation 2.

This gives

`\begin{gathered} P(t)=0.9t^2+6t+23000\text{ } \\ P(9)=0.9(9)^2+6(9)+23000\text{ } \\ =72.9+54+23000=23126.9 \\ \therefore P(9)=23127\text{ (nearest person)} \end{gathered}`

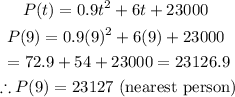
Hence, the population of Pleasantburg on January 1, 2021 is 23127 (nearest person).