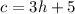Answer:
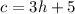
Explanation:
This situation can be represented by a linear function since it has a constant rate of change, linear functions are represented by the following equation:
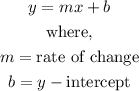
To determine the rate of change of the function, we can use the following expression:

We have the following given points: (0,5) and (1,8):

The y-intercept is where the functions cross the y-axis, which means x=0.
In the table, we can see that the y-intercept of this function would be 5.
Therefore, the equation that represents this relationship between cost, c, and the number of hours h: