Question

what is an equation of the line that passes through the point (-1,2) and is parallel to the line 3x+y=3

Answer 1

y = -3x - 1

Step-by-step explanation:

Given the below equation of a line;

`3x+y=3`

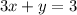
But we know that the slope-intercept form of the equation of a line is given as;

`y=mx+b`

where m = slope and b = y-intercept

Let's go ahead and rearrange the given equation in the question to look like our slope-intercept form of the equation of a line;

`y=-3x+3`

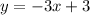
Comparing with the slope-intercept form of the equation of a line, we can see that the slope(m) is -3.

Any line that will be parallel to this line will have the same slope because parallel lines always have the same slope.

Knowing that the slope(m) of the required line is -3, let's go ahead find find the equation of the parallel line that will pass through the points (-1, 2). Note that the x-value of the coordinate is -1 and the y-value is 2.

Let's use the point-slope form of the equation of a line;

`y-y_1=m(x-x_1)`

Let's substitute our known values, m = -3, y1 = 2, and x1 = -1;

`\begin{gathered} y-(2)=-3(x+1) \\ y-2=-3x-3 \\ y=-3x-3+2 \\ y=-3x-1 \end{gathered}`

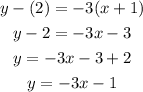
Therefore, the required equation of the line is y = -3x - 1