Question

1. There were 330 people at a play. the admission price was $3 for adults and $1 for children. the admission receipts were $650. how many adults and how many children attended? A) Children: 170, Adults: 60B) Children: 30, Adults: 300C) Children: 160, Adults: 170D) Children: 170, Adults: 160

Answer 1

`D)\text{Children:}170\text{ , Adults :160}`

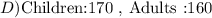
Step-by-step explanation

Step 1

Set the equations

let x represents the number of adults attended

let y represents the number of children attended

so

There were 330 people at a play:

it means the sum of adults and children is 330

`x+y=330\Rightarrow equation(1)`

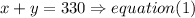
and

if the admission price for $3 for adults, the money from the adult tickets is

`3x`

and $1 for children

`1y`

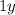
admission receipts were $650,hence

`\begin{gathered} 3x+y=650\Rightarrow equation(2) \\ \end{gathered}`

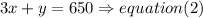
Step 2

solve the equations

`\begin{gathered} x+y=330\Rightarrow equation(1) \\ 3x+y=650\Rightarrow equation(2) \\ \end{gathered}`

a) isolate y in equation (1) and replace in equation (2)

`\begin{gathered} x+y=330\Rightarrow equation(1) \\ \text{subtract y in both sides} \\ x+y-y=330-y \\ x=330-y \\ \text{Now , replace in equation (2)} \\ 3x+y=650\Rightarrow equation(2) \\ 3(330-y)+y=650 \\ 990-3y+y=650 \\ 990-2y=650 \\ \text{subtract 990 in both sides} \\ 990-2y-990=650-990 \\ -2y=-340 \\ divide\text{ both sides by -2} \\ (-2y)/(-2)=(-340)/(-2) \\ y=170 \end{gathered}`

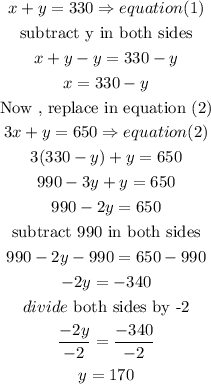
therefore

170 childrend attended

b) now, to find x, replace the y value in equation (1)

`\begin{gathered} x+y=330\Rightarrow equation(1) \\ x+170=330 \\ \text{subtract 170 in both sides} \\ x+170-170=330-170 \\ x=160 \end{gathered}`

Therefore,

160 adults attended

so, the answer is

`D)\text{Children:}170\text{ , Adults :160}`

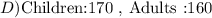
I hope this helps you