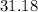Question

Find the exact value and the approximate value of the area of the triangle

Answer 1

From the big triangle we know that:

`\begin{gathered} x^2+y^2=12^2 \\ x^2+y^2=144 \end{gathered}`

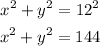
From the triangle on the right we also know that:

`h^2+9^2=y^2`

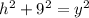
From the triangle on the left we know:

`3^2+h^2=x^2`

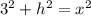
Adding the last two equations we have that:

`\begin{gathered} x^2+y^2=h^2+9^2+h^2+3^2 \\ x^2+y^2=2h^2+90 \end{gathered}`

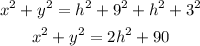
Equating the last equation with the first one we have that:

`\begin{gathered} 2h^2+90=144 \\ 2h^2=144-90 \\ 2h^2=54 \\ h^2=(54)/(2) \\ h^2=27 \\ h=\sqrt[]{27} \end{gathered}`

Then, the height of the triangle is the squared root of 27.

Once we know the height we can calculate the area.

`\begin{gathered} A=(1)/(2)bh \\ =(1)/(2)12\sqrt[]{27} \\ =6\sqrt[]{27} \end{gathered}`

Therefore the exact value of the area is:

`6\sqrt[]{27}`

This can be approximated to (rounding on the hundreths):

`31.18`