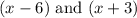Question

The area of a rectangle is x^2-3x-18.What are the dimensions?

Answer 1

Factor the trinomial to find a possible combination of dimentions that the rectangle could have:

`x^2-3x-18`

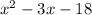
To factor the trinomial, remember that the following product of binomials is equal to:

`(x+a)(x+b)=x^2+(a+b)x+ab`

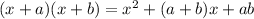
Then, we need to find two numbers a and b such that their product is equal to the constant term -18 and their sum is equal to the linear coefficient -3.

Since the product is negative, one number is negative and the other is positive.

Since the sum is negative, the greatest number is negative.

Two numbers whose difference is 3 and whose product is 18 are 6 and 3.

Notice that:

`\begin{gathered} -6+3=-3 \\ (-6)(3)=-18 \end{gathered}`

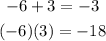
Then:

`x^2-3x-18=(x-6)(x+3)`

Therefore, the dimensions of the rectangle, are:

`(x-6)\text{ and }(x+3)`