Question

Which set of points shown on the complex plane gives the solution to the equation 4^2 +36=0

Answer 1

B. Q and S

Explanation:

Given the below equation;

`4x^2^{}+36=0`

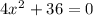
We'll follow the below steps to solve the above equation;

Step 1: Subtract 36 from both sides of the equation;

`\begin{gathered} 4x^2+36-36=0-36 \\ 4x^2=-36 \end{gathered}`

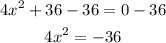
Step 2: Divide both sides of the equation by 4;

`\begin{gathered} (4x^2)/(4)=-(36)/(4) \\ x^2=-9 \end{gathered}`

Step 3: Take the square root of both sides;

`\begin{gathered} x=\pm\sqrt[]{-9} \\ x=\pm\sqrt[]{-1*9} \\ x=\pm(\sqrt[]{-1}*\sqrt[]{9}) \\ Note\text{ that i = }\sqrt[]{-1} \\ x=\pm(i*\sqrt[]{9}) \\ x=\pm3i \end{gathered}`

We can see that the solutions are imaginary numbers so we'll need to plot the two points on the imaginary axis, so points Q and S give the solutions to the given equation.