Answer:
The correct option is C
There are no possible solutions to the triangle
Step-by-step explanation:
The sides of the triangle can be obtained using Cosine Rule as follows:
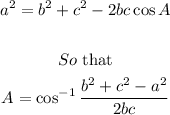
Using the given parameters, we have:
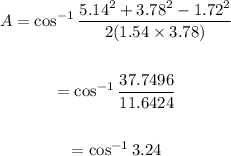
The last line is impossible
We conclude that there are no possible solutions for the triangle