1 Answer

Byronyasgur · Answer 1 · 2023-08-26T10:56:44+0000

The question is given below as

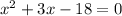
Step 1:We will look for two factors we will multiply together to get -18 and the same two factors that will add up together to +3

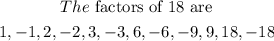
$\begin{gathered} The\text{ factors of 18 are} \\ 1,-1,2,-2,3,-3,6,-6,-9,9,18,-18 \end{gathered}$

Since -18 is a negative value

Then, the two factors must have different signs because of the sign pattern below

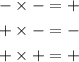
$\begin{gathered} -*-=+ \\ +*-=- \\ +*+=+ \end{gathered}$

The two factors are

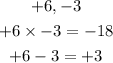
$\begin{gathered} +6,-3 \\ +6*-3=-18 \\ +6-3=+3 \end{gathered}$

Step 2: Substitute the factors in the equation below

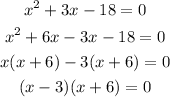
$\begin{gathered} x^2+3x-18=0 \\ x^2+6x-3x-18=0 \\ x(x+6)-3(x+6)=0 \\ (x-3)(x+6)=0 \end{gathered}$

Step 3: Equate both factors to zero

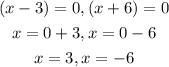
$\begin{gathered} (x-3)=0,(x+6)=0 \\ x=0+3,x=0-6 \\ x=3,x=-6 \end{gathered}$

Hence,

The final answer are x =3 and x = -6

Please log in or register to add a comment.