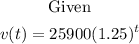
Part A: Finding the initial value of the car
Substitute t = 0 to the given function and solve for v(t)
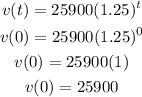
Therefore, the initial value of the car is $25,900.
Part B: Growth or Decay
Since the base of the exponential function is greater than 1, in this case 1.25, the function represents growth.
Part C: Percent change every year
Subtract 1 from the base 1.25, and multiply by 100%
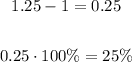
Therefore, the percent change each year is 25%.