Question

Find the greatest common factor of the following monomials2b^4 32b^6 22b^5

Answer 1

The answer is

`2b^4`

First let's see the divider of the coeficient:

2 is a prime

32 = 2^5 = 2*2*2*2*2

22 = 11*2

The GCD of all is 2

Now, we have b to the 4, 5 and 6. We can write it:

`\begin{gathered} b^6=b^4\cdot b^2 \\ b^5=b^4\cdot b \end{gathered}`

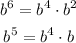
Now we have all to get the answer:

`\begin{gathered} 32b^6=2^4b^2\cdot(2b^4) \\ 22b^5=11b\cdot(2b^4) \end{gathered}`

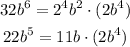
And the remaining is 2b^4. As you can see, all the monomyals can be divided by 2b^4 and that's the greatest common factor