Question

The owner of a new restaurant is designing the floor plan, and he is deciding between two different seating arrangements. The first plan consists of 23 tables and 25 booths, which will seat a total of 242 people. The second plan consists of 23 tables and 22 booths, which will seat a total of 224 people. How many people can be seated at each type of table

Answer 1

Okay, here we have this:

Considering the provided information, we obtain the following system of equation, let's solve it:

`\begin{gathered} \begin{bmatrix}23x+25y=242 \\ 23x+22y=224\end{bmatrix} \\ \begin{bmatrix}23x+25y=242 \\ (-1)23x+22y=224(-1)\end{bmatrix} \\ \begin{bmatrix}23x+25y=242 \\ -23x-22y=-224\end{bmatrix} \end{gathered}`

Adding the equations:

`\begin{gathered} 3y=18 \\ y=(18)/(3) \\ y=6 \end{gathered}`

Now, let's replace this value in the first function to find the value of x:

`\begin{gathered} 23x+25y=242 \\ 23x+25(6)=242 \\ 23x+150=242 \\ 23x=242-150 \\ 23x=92 \\ x=(92)/(23) \\ x=4 \end{gathered}`

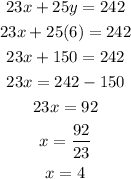
Finally we obtain that 4 people can sit at each table and 6 people at each booth.