Question

The annual interest on an $20,000 investment exceeds the interest earned on an $8000 investment by $660. The $20,000 is invested at a 0.6% higher rate of interest than the $8000. What is the interest rate of each investment?

Answer 1

Given: The annual interest on a $20,000 investment exceeds the interest earned on an $8000 investment by $660.The $20,000 is invested at a 0.6% higher rate of interest than the $8000.

Required: To find the interest rate of each investment.

Explanation: Let the interest rate for $20000 be x and for $8000 investment be y.

Then according to the question

`20000* x=8000* y+660\text{ ...\lparen1\rparen}`

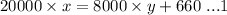
and

`\begin{gathered} x=y+0.6\% \\ x=y+0.006\text{ ...\lparen2\rparen} \end{gathered}`

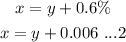
Substituting this value of x in equation (1) we get

`\begin{gathered} 20000(y+0.006)=8000y+660 \\ 20000y-8000y=680-120 \\ 12000y=560 \\ y=(560)/(12000) \\ \end{gathered}`

Which gives y=0.0466

So the $8000 investment is invested at 4.66%.

Also

`\begin{gathered} x=y+0.006 \\ =0.0466+0.006 \\ =0.0526 \end{gathered}`

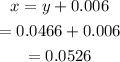
Hence the $20000 is invested at 5.26%.

Final Answer: The interest rate for $20000 is 5.26% and for $8000 is 4.66%.