As per given by the question,
There are given that cups are 3 inches wide and 2 inches tall.
Now,
For finding the height of cone,
Here use formula of the height of cone.
So,
There are given diameter is 3 inches, and 2 inches tall .
Now,
First find the volume of right circular,
Then,
From the formula of right circula volume,
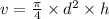
Then, substitute the value in above formula,
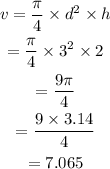
Now,
Let us consider the height of cone is h.
it is given that width of the cone is equal to cup.
So,
Diameter is given that is 3.
So,
From the formula of the volume of the cone,
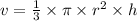
Put the value of v, and radius r in the above formula to find the,
So, here radius is,
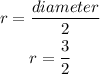
Then,
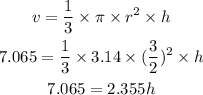
Now, solve for h;

Hence, the height of the cone is 3 inc.