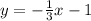Question

Write the equation of the line that is parallel to y = -1/3X - 2through the point (9,-4).Point-Slope FormSlope-Intercept Form

Answer 1

The equation of the line is:

`y=-(1)/(3)x-1`

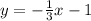
Step-by-step explanation:

Given that the line is parallel to the line;

`y=-(1)/(3)x-2`

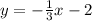
Since the two lines are parallel, they must have the same slope.

So, the slope of the line is;

`m=-(1)/(3)`

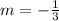
Also, given that the line passes through the point;

`(x_1,y_1)=(9,-4)`

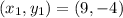
Applying the point-slope equation;

`y-y_1=m(x-x_1)`

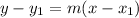
substituting the given values, we have;

`\begin{gathered} y-(-4)=-(1)/(3)(x-9) \\ y+4=-(1)/(3)x+(1)/(3)(9) \\ y+4=-(1)/(3)x+3 \\ y=-(1)/(3)x+3-4 \\ y=-(1)/(3)x-1 \end{gathered}`

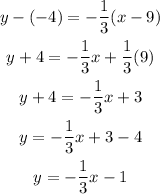
Therefore, the equation of the line is;

`y=-(1)/(3)x-1`