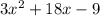Question

hola buenos días que tal como esta espero me pueda ayudar y si me salgo es porque tuve un problema y disculpe

Answer 1

Since the problem states to substract from the second polynomial given the problem that we will be solving is

`(7x^2+6x)-(2x-3)^2`

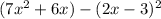
continue by solving the expression that is squared using the definition

`(a-b)^2=a^2-2\cdot a\cdot b+b^2`

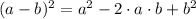
applying this to the expression given

`\begin{gathered} (2x-3)^2=(2x)^2-2\cdot(2x)\cdot(3)+(3)^2 \\ (2x-3)^2=4x^2-12x+9 \end{gathered}`

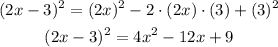
insert this into the first expression

`\begin{gathered} (7x^2+6x)-(2x-3)^2 \\ (7x^2+6x)-(4x^2-12x+9) \end{gathered}`

distribute the negative sign

`(7x^2+6x)-4x^2+12x-9`

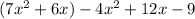
simplify the expression

`3x^2+18x-9`