Question

WITHOUT using a graphing device, find the x- and y- intercepts of the graph :

Answer 1

Given:

The equation of graph is given as,

`y=x^3-2x^2+x`

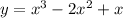
The objective is to find x intercepts and y intercepts without using graph.

Step-by-step explanation:

To find y intercept:

If the graph passes through the y axis, the value of x will be zero.

At x = 0,

`\begin{gathered} y=0^3-2(0)^2+0 \\ y=0 \end{gathered}`

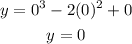
Thus, the y intercept is (0,0).

To find x intercept:

If the graph passes through the x axis, the value of y will be zero.

At y = 0,

`0=x^3-2x^2+x`

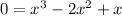
By rearranging and grouping the above equation,

`\begin{gathered} 0=x(x^2-2x+1) \\ 0=x(x^2-x-x+1) \\ 0=x\lbrack x(x-1)-1(x-1)\rbrack \\ 0=x(x-1)(x-1) \end{gathered}`

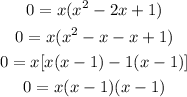
On solving the above equation by splitting into two terms,

`\begin{gathered} x=0 \\ x-1=0\text{ or x=1} \end{gathered}`

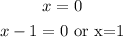
Thus, the x intercepts are (0,0) and (1,0).

So, the obtained x intercept is (0,0), (1,0) and the y intercept is (0,0).

Hence, option (d) is the correct answer.