Question

Which of the following polynomial equations are valid A. m³-1=(m-1) (1+m+m²)B. (n+3)²+2n=8n+13A) both A and B B) only BC) neither A nor BD) only A

Answer 1

Check the validity of each equation using the properties of the real numbers to see if they are true or false.

A

Starting with the expression:

`(m-1)(1+m+m^2)`

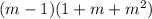
Use the distributive property to expand the second factor:

`\begin{gathered} (m-1)(1+m+m^2) \\ =(m-1)(1)+(m-1)(m)+(m-1)(m^2) \end{gathered}`

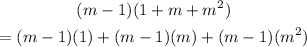
Use the same property to expand the factor (m-1) in each term. Simplify the expression:

`\begin{gathered} (m-1)(1)+(m-1)(m)+(m-1)(m^2) \\ =(m-1)+(m\cdot m-1\cdot m)+(m\cdot m^2-1\cdot m^2) \\ =m-1+m^2-m+m^3-m^2 \end{gathered}`

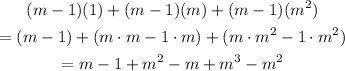
Notice that the term m cancels out with the term -m, and the term m^2 cancels out with the term -m^2. Therefore:

`m-1+m^2-m+m^3-m^2=-1+m^3`

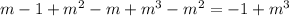
Therefore:

`(m-1)(1+m+m^2)=m^3-1`

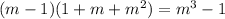
Therefore, the equation A is true.

B

Expand the term (n+3)^2 and add 2n to see if it is equal to 8n+13.

`\begin{gathered} (n+3)^2+2n \\ =(n^2+2\cdot3\cdot n+3^2)+2n \\ =(n^2+6n+9)+2n \end{gathered}`

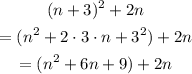
Add the like terms 6n and 2n:

`\begin{gathered} (n^2+6n+9)+2n \\ =n^2+8n+9 \end{gathered}`

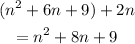
Which cannot be equal to 8n+13 since there is a quadratic term.

Therefore, the equation B is false.