ANSWER
c). Two and half years (2.5 years).
Step-by-step explanation
Given:
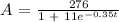
Desired Outcome:
The number of years it will take for the herd to grow to 50 deer
Determine time 't'
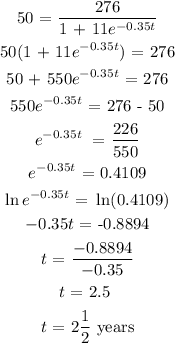
Hence, it will take two and half (2.5) years for the herd to grow to 50 deer.