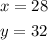Solution
- The figure given is a Kite. Based on this, there are some properties we need to know in order to solve the question
1. The Opposite Obtuse angles are equal.
2. The longer diagonal divides the kite into two congruent triangles (That is, the triangles have equal angles and sides).
- With the above properties we can proceed to solve the question
Applying Property 1:
- The Opposite Obtuse angles are equal. This implies that the angles highlighted below are equal:
- Thus, we can write
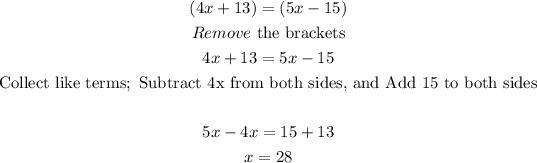
- The value of x is 28°
Applying Property 2:
- The longer diagonal divides the kite into two congruent triangles.
- This implies that the angles on both triangles formed by that large diagonal are equal. That is,
- Now that we have established the following, we can simply pick any of the triangles and apply the "sum angle theorem" on any of them.
- This is done below:

- The value of y is 32°
Final Answer
The values of x and y are: