Question

Suppose you want to solve the equation 4a +b =4a, where a and b are nonzero real numbers.Complete the explanation.If you subtract 4a from each side, you get the statement b = a Since a and b are(select)this statement is (select). Therefore, there is (select) solution.

Answer 1

We have the following equation:

`4a+b=4a`

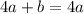
If we subtract 4a from both sides, we have:

`\begin{gathered} 4a+b-4a=4a-4a \\ (4a-4a)+b=(4a-4a) \\ b=0 \end{gathered}`

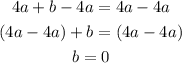
If you subtract 4a from each side, you get the statement b = 0. Since a and b are nonzero real numbers this statement is false. Therefore, there is no solution.

We started the question with the following statement:

"Suppose you want to solve the equation 4a +b =4a, where a and b are nonzero real numbers."

By solving the equation, we found out that 'b' MUST be zero. Since 'b' must be zero, this statement can't be fullfilled, because it requires for 'a' and 'b' to be nonzero real numbers.

Therefore, the statement is false, and the reason the statement is false is because 'b' can't be nonzero. Since we can't solve this equation and fullfill the statement at the same time, this problem has no solution.