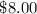Given that:
- Kyra is framing a square painting with side lengths (in inches) of:
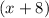
- The total area of the painting and the frame has a side length (in inches) of:
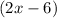
• You need to remember the formula for calculating the area of a square is:
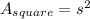
Where "s" is the side length of the square.
Therefore, you can determine that the area of the square painting (in square inches) is:
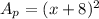
And the total area (in square inches) of the square frame and the square painting is:

Therefore, the area of the frame is the Difference between them:
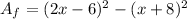
You can simplify the area as follows:
1. Apply this formula:
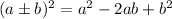
Then:
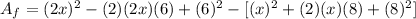
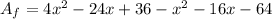
2. Add the like terms:
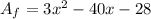
• You know that the material for the frame will cost $0.08 per square inch. Then, in order to find the cost of the material is:
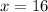
You first need to substitute that value into the equation for the area of the frame and evaluate:

Multiply the cost $0.08 by that area:
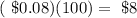
Hence, the answer is:
- Expression for the area of the frame:
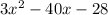
- Cost of the material for the frame: