We will assume here that we have a right triangle to solve the question.
We have the following triangle:
To find the diagonal, d, we can use the Pythagorean Theorem, which says that, in a right triangle, the sum of the square of the length of each side of the triangle is equal to the square of the hypotenuse. or:

In this case, we have:
• c ---> d
,
• a = 24 ft
,
• b = 7 ft
Then, we have:
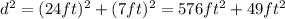
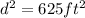
Taking the square root to both sides of the equation, we have:
![\sqrt[]{d^2}=\sqrt[]{625ft^2}\Rightarrow d=25ft](https://img.qammunity.org/2023/formulas/mathematics/college/9rbcr42bjvw7hh64k0my4vb1jrspwc4fkk.png)
Therefore, the value for d is equal to 25 ft (25 feet).