To solve the exercise you can use the following properties of rhombuses:
*AB = BC = CD = AD
*BO = OD and AO = OC
Now, as you can see the triangle COD is a right triangle, then you can use the trigonometric ratio cos (θ) to find the measure of the segment OD:
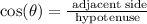
Then, you have
![\begin{gathered} \cos (50\text{\degree)}=(OD)/(CD) \\ \cos (50\text{\degree)}=\frac{OD}{5\operatorname{cm}} \\ \text{ Multiply by 5 cm on both sides of the equation} \\ \cos (50\text{\degree)}\cdot5cm=\frac{OD}{5\operatorname{cm}}\cdot5\operatorname{cm} \\ \cos (50\text{\degree)}\cdot5cm=OD \\ 3.2\operatorname{cm}=OD \end{gathered}]()
Finally, as BO = OD so, you have
![\begin{gathered} BD=BO+OD \\ BD=3.2\operatorname{cm}+3.2\operatorname{cm} \\ BD=6.4\operatorname{cm} \end{gathered}]()
Therefore, the length of diagonal BD is 6.4 cm.