Question

Find the volume of the following composite figure. 12 in. 13 in. A. 2,374 in B. 716 in C. 1,922 in D. 11,304 in

Answer 1

In this question, we have a composite figure. We can figure out that the composite figure is half of a sphere with a diameter of 12 inches and a cylinder with a height of 13 inches and a base with the same diameter.

Then, we have to calculate the volume of the sphere:

The radius of the sphere and the cylinder is 12/2 = 6 inches.

`V_{\text{sphere}}=(4)/(3)\cdot\pi\cdot r^3=(4)/(3)\cdot\pi\cdot6^3=904.78in^3`

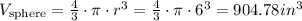
Since we have half of the sphere, we need to divide the previous result by 2:

`V_{\text{semisphere}}=(904.78in^3)/(2)=452.39in^3`

Now, we need to find the volume of the cylinder:

`V_{\text{cylinder}}=\pi\cdot r^2\cdot h=\pi\cdot(6)^2\cdot13=1470.27in^3`

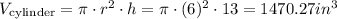
Now, we need to sum both volumes:

Total volume = 452.39 in^3 + 1470.27 in^3 = 1922.66 in^3 (option C.)