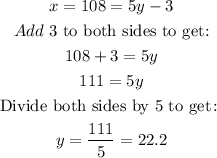Question

Each figure consists of two parallel lines and a transversal.Find each angle measure and identify each pair of angles as (Alt interior, corresponding, same sideinterior)ful5. measure of angle 16. identify

Answer 1

5) Angle 1 = 140 degrees.

When two parallel lines are cut across by a transversal, there will be a pair of corresponding angles which are equal.

6) Corresponding angles.

7) We have another case of corresponding and alternate angles.

`\begin{gathered} 112=4x\text Both are Corresponding angles \\ \text{Divide both sides by 4 to get:} \\ x=(112)/(4)=28 \end{gathered}`

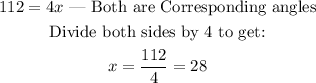
8) y = 112 degrees. | Both are alternate angles

9) 72 degrees and x are supplementary (adds up to 180 degrees)

`\begin{gathered} 72+x=180 \\ \text{Subtract 72 from both sides to get:} \\ x=180-72=108^o \end{gathered}`

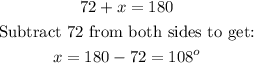
10) x and (5y - 3) are corresponding angles and are therefore equal.

`\begin{gathered} x=108=5y-3 \\ Add\text{ 3 to both sides to get:} \\ 108+3=5y \\ 111=5y \\ \text{Divide both sides by 5 to get}\colon \\ y=(111)/(5)=22.2 \end{gathered}`