We have a triangle with the following side lengths
6, 11, and 14
Let a = 6, b = 11, and c = 14
A triangle is said to be an "acute" triangle if the following relation holds true
![c^2Let us check if the above relation is true or not[tex]\begin{gathered} 14^2<6^2+11^2 \\ 196^{}<36^{}+121^{} \\ 196<157 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bzrcr47thcezx4fvmmxnvyb7xfwlry0zql.png)
As you can see, the above relation is not true.
This is rather "obtuse" triangle
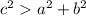
The above relation holds true in this case
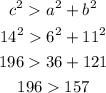
So, this obtuse triangle will look like below
The angle opposite the longest side will be greater than 90°