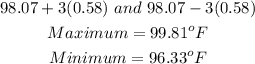SOLUTION;
Using Chebyshev's theorem the percentage of healthy adults with body temperatures that are within 3 standard deviations of the mean make up at least 89% of the population.
Thus;
The maximum and minimum possible body temperatures that are within 3 standard deviations of the mean are;