Question

Two different functions are represented by this graph and this table:X0А.1By1471316245Which linear function has a greater slope?САThe slopes are equal

Answer 1

Step 1: Write out the formular for slope

`\text{Slope(m)}=\frac{Change\text{ in y}}{\text{Change in x}}=\text{ }(y_2-y_1)/(x_2-x_1)`

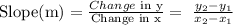
Step 2: Solving for the slope of A

`\begin{gathered} \text{Where y}_1=\text{ 0} \\ y_2=\text{ 3} \\ x_1=\text{ 0} \\ x_2=\text{ -1.5} \\ m=\text{ }(3-0)/(-1.5-0) \\ m=\text{ }(3)/(-1.5) \\ m=\text{ -2} \end{gathered}`

The slope of A is -2

Step 3: Pick any two points from the vale s of B given and finding the slope,

The two points which I want to pick are, when x1= 0, x2=1, y1=1, y2=4.

`\begin{gathered} \text{The slope(m) of B} \\ m=\text{ }(4-1)/(1-0)=(4)/(1) \\ m=4 \end{gathered}`

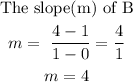
Therefore the slope of B, m is 4.

Step 4: Comparing the slope of A and B to check which one is of greater slope.

From the solution of slope for A and B done above where the slope of A is -2 and the slope of B is 4, we can deduce that function B is of greater slope.

Hence, the option is B.