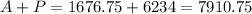Question

Francine wants to invest $6,234 at a rate of 5.25% compounded weekly. How much will be in her account after 25 years? Round to the nearest penny.

Answer 1

To calculate the final amount on an account with compound interest you have to use the following formula:

`A=P(1+(r)/(n))^(nt)`

Where

A is the accrued amount

P is the principal amount

r is the interest rate expressed as a decimal value

t is the time involved

n is the number of compounding periods per unit of t.

In this exercise, the account compounds weekly, there are 52 weeks in one year, so per year, there will be 52 compounding periods → n=52

The principal amount is the money you want to invest P=$6234

To express the interest rate as a decimal value you have to divide the given percentage by 100

`r=(5.25)/(100)=0.0525`

And the time lapse of the investment is t=25 years

Replace the formula with the data to calculate the accrued

`\begin{gathered} A=6234(1-(0.0525)/(52))^(52\cdot25) \\ A=6234(1-(0.0525)/(52))^(1300) \\ A=1676.75 \end{gathered}`

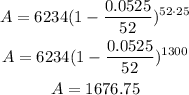
The total amount after 25 years is the accrued amount plus the principal investment

`A+P=1676.75+6234=7910.75`