Given:
a.) A 12-tooth gear on a motor shaft drives a larger gear having 30 teeth.
b.) The motor shaft rotates at 500 rpm.
For us to be able to determine the speed of the larger gear, we will be using the gear ratio formula:
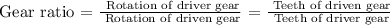
In this scenario, the driver gear is the 12-tooth gear and the driven gear is the larger gear with 30 teeth.
We get,
Let x = the speed of the larger gear
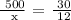
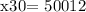
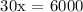
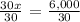
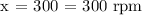
Therefore, the speed of the larger gear is 300 rpm.