Answer:
7.19 m/s
Step-by-step explanation:
By the work-energy theorem, we have the following equation
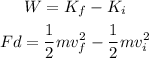
Where F is the force, d is the distance, m is the mass, vf is the final speed and vi is the initial speed. Solving for vf, we get
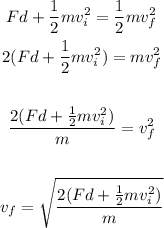
Replacing F = 72.5 N, d = 15.6 m, m = 45.3 kg, and vi = 1.31 m/s, we get

Therefore, the final speed of the sled was 7.19 m/s