Question

Brian has two rectangular gardens that have the same area but different perimeters. Each garden has an area of 48 square feet. Draw two different rectangles with an area of 48 square feet but with different perimeters. Include the dimensions of your rectangle. Then, determine which of your designs will require less fencing and explain.

Answer 1

The area of both rectangular gardens is

`A=48ft^2`

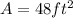
The area of a triangle is calculated using the formula below

`\begin{gathered} A=l* b \\ l=8ft,b=6ft \end{gathered}`

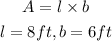
The area of garden B can be represented below as

`\begin{gathered} A=l* b \\ l=12ft,b=4ft \end{gathered}`

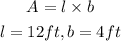
To figure out the garden design that requires less fencing, we will have to calculate the perimeter of both gardens below using the formula below

The perimeter of GARDEN A will be

`\begin{gathered} P=2(l(+b) \\ P=2(8ft+6ft) \\ P=2(14ft) \\ P=28ft \end{gathered}`

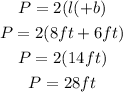
The Perimeter of GARDEN B will be

`\begin{gathered} P=2(l+b) \\ P=2(12FT+4FT) \\ P=2(16ft) \\ P=32ft \end{gathered}`

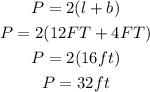
Hence,

Garden A will require less fencing because it has the less perimeter