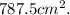Question

15 cm14cm23 cm19 cm34 cm

Answer 1

To determine the area of the figure, we will compute the area of the parallelogram and the area of the trapezoid.

Recall that the area of a parallelogram is given by the following formula:

`A=base*height.`

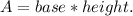
Therefore, the area of the parallelogram is:

`A=14cm*23cm=322cm^2.`

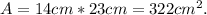
Now, the area of a trapezoid is given by the following formula:

`A=(base+Base)/(2)*height.`

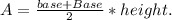
Therefore, the area of the trapezoid is:

`A=(34cm+15cm)/(2)*19cm=465.5cm^2`

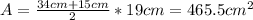
Finally, we get that the area of the whole figure is:

`322cm^2+465.5cm^2=787.5cm^2.`

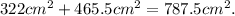
Answer:

`\begin{equation*} 787.5cm^2. \end{equation*}`