Question

A park ranger wants to calculate the length of a lake. Starting at one end of the lake, the park ranger walks 200 feet, then turns 100º, and walks another 225 feet as shown in the figure below. Find the length of the lake (x). Show all work clearly and neatly. Round to the nearest tenth.

Answer 1

`x\text{ = 273.9 ft}`

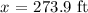
Step-by-step explanation:

Here, we want to get the value of the side marked x

From what we have, we can use the cosine rule to get it

But before we use the rule, we need to know the value of the interior angle that faces x

To get this, we have to subtract the value of theexternal angle from 180

This is because the external angle and the angle that faces x are supplementary (they add up to 180 degrees) since they lie on a straight line

The value of this angle is thus:

`180-100\text{ = 80}`

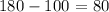
Now,we can proceed to use the cosine rule

In the general form,we have the cosine rule as:

`a^2=b^2+c^2\text{ -2bc}\cdot Cos\text{ A}`

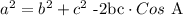
With respect to the values given,the sides b and c are the other sides, x is a and A is the angle that faces x which has been written above

Substituting these values, we have it that:

`\begin{gathered} x^2\text{ }=225^2+200^2-2(225)(200)Cos80 \\ x^2\text{ = 74,997} \\ x\text{ = }\sqrt[]{74997} \\ x\text{ = }273.9\text{ }ft \end{gathered}`