Question

Which equation is perpendicular to y= 1/2x + 4 *y= 1/2x - 3y= -1/2x + 7y= -2x + 4y= 2x + 4

Answer 1

y = -2x + 4

Explanations:

Given the equation of a line expressed as y = 1/2x + 4

For two lines to be perpendicular to each other, the product of their slope is -1

Let m₁ and m₂ be the slopes of the line, if the lines are perpendicular, then;

`m_1m_2=-1`

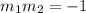
Since the slope of the given equation is 1/2, hence:

`(1)/(2)m_2=-1`

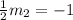
Cross multiply to determine m₂

`\begin{gathered} m_2=-1*2 \\ m_2=-2 \end{gathered}`

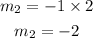
This shows that the slope of the equation that is perpendicular must be -2. Hence from the given option, the equation perpendicular to y = 1/2x + 4 will be y = -2x + 4