Question

How do I solve the following word problem: The half-life of Phosphorus - 32 is 14.3 days. It is used to study a plant's use of fertilizers. A) Write an exponential decay function for a 50mg sample. b) Find the amount of P - 32 remaining after 84 days.

Answer 1

Half life is the time that it takes for half of the original value of some amount of a radioactive element to decay.

We have the following equation representing the half-life decay:

`A=A_o*2^{(-(t)/(t_(half)))_{}_{}}`

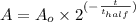
A is the resulting amount after t time

Ao is the initial amount = 50 mg

t= Elapsed time

t half is the half-life of the substance = 14.3 days

We replace the know values into the equation to have an exponential decay function for a 50mg sample

`A=\text{ 50 }*2^{(-t)/(14.3)}`

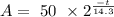
That would be the answer for a)

To know the P-32 remaining after 84 days we have to replace this value in the equation:

`\begin{gathered} A=\text{ 50 }*2^{(-84)/(14.3)} \\ A=0.85\text{ mg} \end{gathered}`

So, after 84 days the P-32 remaining will be 0.85 mg