Question

Look at the picture provided to see the problem.Answer the questions below(choose only one answer per question)1. The series A. converges B. diverges 2. You know this because the series is A. arithmetic B. geometric and the common ratio is 0.2.C. geometric and the common ratio is 2.

Answer 1

A. Converges

B. geometric and the common ratio is 0.2

Given the sequence,

`1000+200+40+8+(8)/(5)+\cdots`

we can determine whether it diverges or converges by finding the ratio of the given geometric sequence.

If:

|r| < 1, the series converges.

|r| ≥ 1, the series diverges.

We can find the ratio r by dividing a term by the previous term. For instance,

`(200)/(1000)=0.2`
`(40)/(200)=0.2`
`(8)/(40)=0.2`

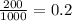
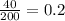
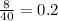
Now that we know that the ratio is 0.2,

`|r|=|0.2|=0.2,0.2<1_{}`

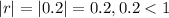
This means that the series converges, and we know it because the series is geometric and the common ratio is 0.2.