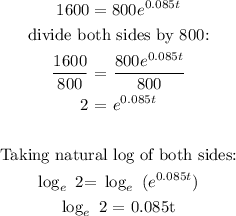8.2 years
Step-by-step explanation:
Initial amount = $800
Doubling the amount = 2(800) = $1600
Future amount = double the amount = $1600
rate = 8.5% = 0.05
time = t = ?
n = compounded continously
The function is given as:
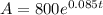
We need to find the time given the amount is $1600: