Question

The sum of the first 10 terms of an arithmetic progression is 40. If the first term is -5, then what is the common difference?-3-124

Answer 1

Given data:

The sum of the first 10 terms of an arithmetic progression = 40

The first term is -5

Using the formula to get the sum of an arithmetic term

`S_n=(n)/(2)\lbrack2a+(n-1)d\rbrack`

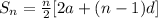
from the above formula

`\begin{gathered} a=-5 \\ n=10 \\ S_n=40 \\ d\text{ is unknown} \end{gathered}`

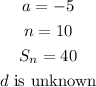
Method: substitute the values and make d the subject of the formula

`40=(10)/(2)\lbrack2*-5+(10-1)* d\rbrack`

=>

`40=5(-10+9d)`

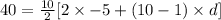
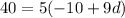
=> divide both sides by 5

`(40)/(5)=(5(-10+9d))/(5)`

=>

`8=-10+9d`

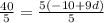
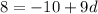
=> collect like terms

9d=10+8

=>

9d=18

=>Divide both sides by 9

`d=(18)/(9)=2`

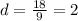
Therefore the common difference is 2