1 Answer

Richard Morgan · Answer 1 · 2023-07-03T15:22:36+0000

It is given that

A stone is thrown into a pond, A circular ripple spreads over the pond in such a way that the radius is increasing at a rate of 2.5 feet per second.

In one second the increment in radius is 2.5 feet

After t seconds, the increment in radius is given by

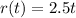
The area of the circular ripple is

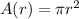
$A(r)=\pi r^2$

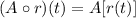
$(A\circ r)(t)=A\lbrack r(t)\rbrack$

Substitute r(t)=2.5t, we get

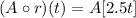
$(A\circ r)(t)=A\lbrack2.5t\rbrack$

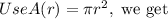
$UseA(r)=\pi r^2,\text{ we get}$

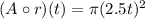
$(A\circ r)(t)=\pi(2.5t)^2$

The required function is

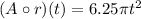
$(A\circ r)(t)=6.25\pi t^2$

Hence the fourth option is correct.

Please log in or register to add a comment.