Question

Which inequality represents all values of x for which the quotient below is defined?A.-2 x 5B.x -2C.-2 x < 5D.x 5

Answer 1

The quotient is given to be:

`√(x+2)/ √(5-x)`

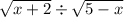
Rewrite the expression:

`\Rightarrow(√(x+2))/(√(5-x))=\sqrt{(x+2)/(5-x)}`

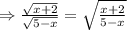
The quotient will be defined under the following condition:

`(x+2)/(5-x)\ge0`

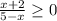
The inequality will work if:

`x+2\ge0\text{ or }5-x\ge0`

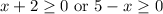
Hence, we can get the interval to be:

`\begin{gathered} x\ge-2 \\ or \\ x\leq5 \end{gathered}`

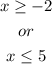
The inequality will be undefined at the point:

`\begin{gathered} 5-x=0 \\ \therefore \\ x=5 \end{gathered}`

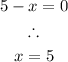
Therefore, the function will be defined over the interval:

`-2\leq x<5`

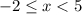
OPTION C is correct.