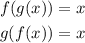Question

Can you please provide a step by step explanation on how to solve this problem?

Answer 1

The exercise wants us to prove that f(g(x)) = x and g(f(x)) = x, then let's prove it.

First, let's start with f(g(x)) = x. Let's do f(g(x)), we must find that it's equal to x.

`\begin{gathered} f(x)=x^2-3 \\ g(x)=√(x+3) \\ \\ f(g(x))=(√(x+3))^2-3 \end{gathered}`

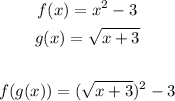
Now we simplify that expression, then

`\begin{gathered} f(g(x))=(√(x+3))^2-3 \\ \\ f(g(x))=x+3-3 \\ \\ f(g(x))=x \end{gathered}`

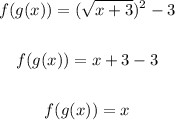
Then we can confirm that f(g(x)) = x. Now let's do the same for g(f(x)), then

`\begin{gathered} g(x)=√(x+3) \\ f(x)=x^2-3 \\ \\ g(f(x))=√((x^2-3)+3) \\ \\ g(f(x))=√(x^2-3+3) \\ \\ g(f(x))=√(x^2) \\ \\ g(f(x))=x \end{gathered}`

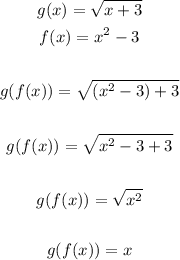
As we expected, it's also true, hence

`\begin{gathered} f(g(x))=x \\ g(f(x))=x \end{gathered}`