Question

What is the name of the shape graphed by the function r = 2 cose? O A. Limaçon with inner loop O B. Lemniscate O C. Line O D. Circle SUBMI

Answer 1

To understand the function better, let's convert it from polar coordinates to cartesian coordinates. The relation between those coordinates are

`\begin{cases}x=r\cos \theta \\ y=r\sin \theta\end{cases}`

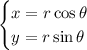
Our function is

`r=2\cos \theta`

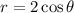
If we multiply both sides by r, we have

`r^2=2r\cos \theta`

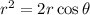
The square of the radius is equal to the sum of the squares of the cartesian coordinates

`x^2+y^2=r^2`

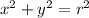
Using this identity, we can rewrite our function as

`x^2+y^2=2x`

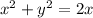
Completing the square, we can rewrite our function as

`\begin{gathered} x^2+y^2=2x \\ x^2+y^2-2x=0 \\ x^2-2x+y^2=0 \\ x^2-2x+1-1+y^2=0 \\ (x-1)^2-1+y^2=0 \\ (x-1)^2+y^2=1 \end{gathered}`

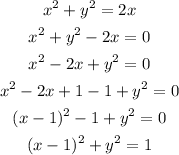
This is a equation of a circle.